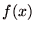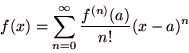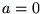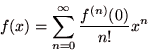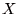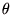モーメント母関数 定義 (テイラー展開) 実数または複素数関数の $f(x)$ が 1変数関数 である場合に テイラー展開 は以下のように定義される． $$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x - a)^{n}$$ (2.7) 定義 (マクローリン展開) $a = 0$ のときの テイラー展開 を マクローリン展開 という． $$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!} x^{n}$$ (2.8) 定義 (モーメント母関数) 離散型確率変数 $X$ と 変数 $\theta$ に対して、モーメント母関数 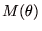$M(\theta)$ は以下のように定義される． $$M(\theta) = E[e^{\theta X}]$$ (2.9) $M(\theta)$ を $\theta$ で微分2.1すると、 $$M'(\theta) = E[X]\cdot\frac{1}{1!}+E[X^{2}]\cdot\frac{2\theta}{2!}+E[X^{3}]\cdot\frac{3\theta^{2}}{3!}+\cdots$$ (2.11) $$= E[X]+E[X^{2}]\cdot\frac{\theta}{2!}+E[X^{3}]\cdot\frac{\theta^{2}}{2!}+\cdots$$ (2.12) $\theta=0$ を代入すると、 $$M'(0)=E[X]$$ (2.13) となる．これはモーメント母関数の1階微分が期待値になることを示している． また、$M(\theta)$ を $\theta$ で2階微分すると、 $$M''(\theta) = E[X^{2}]\cdot\frac{1}{1!}+E[X^{3}]\cdot\frac{2\theta}{2!}+E[X^{4}]\cdot\frac{3\theta^{2}}{3!}+\cdots$$ (2.14) $$= E[X^{2}]+E[X^{3}]\cdot\frac{\theta}{1!}+E[X^{4}]\cdot\frac{\theta^{2}}{2!}+\cdots$$ (2.15) 先と同じように、$\theta=0$ を代入すると、 $$M''(0)=E[X^{2}]$$ (2.16) となる． ここで、確率変数 $X$ の分散を考えると、 $$\sigma^{2}=E[X^{2}]-E[X]^{2}$$ (2.17) である．この式に先のモーメント母関数の結果を代入すると、 $$\sigma^{2}=E[X^{2}]-E[X]^{2}=M''(0)-M'(0)^{2}$$ (2.18) となる．すなわち、確率変数 $X$ の期待値も分散も共にモーメント母関数で表現出来るということになる． 定義 (ネイピア数) 複利計算に関係する以下の数を ネイピア数 という． $$e = \lim_{n \to \infty}\left( 1 + {1 \over n }\right)^n$$ (2.19) 定義 (自然対数) ネイピア数を底とする対数2.2を自然対数という． $$\rm ln x = \log x = \int_1^x {1 \over t}dt$$ (2.21) この関係は、オランダのニコラス・メルカトル(Nicholas Mercator,1620年頃-1687年)によって、1668年に発見された．