
Next: 選好と選択 Up: 離散型確率分布 Previous: モーメント母関数
ベルヌーイ分布(二項分布)の期待値・分散
ベルヌーイ分布の期待値と分散をモーメント母関数と用いて求めてみる.ベルヌーイ分布は、
| (2.22) |
![$\displaystyle E[e^{\theta x}]=\sum_{x=0}^{n}e^{\theta x} \cdot P(x)$](./image/img62.png) |
(2.23) | ||
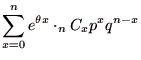 |
(2.24) | ||
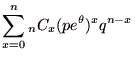 |
(2.25) |
定理 (二項定理 binomial theorem)
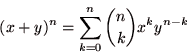 |
(2.26) |
この 二項定理 を用いて、先の結果を変形すると、
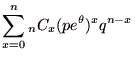 |
(2.27) | ||
| (2.28) |
となる.
この
| (2.29) | |||
| (2.30) |
ここで、
| (2.31) | |||
| (2.32) | |||
| (2.33) | |||
| (2.34) | |||
| (2.35) | |||
| (2.36) |
となる.すなわち、ベルヌーイ分布
さらに、
| (2.37) | |||
| (2.38) | |||
| (2.39) | |||
| (2.40) |
上式に、
| (2.41) | |||
| (2.42) | |||
| (2.43) | |||
| (2.44) | |||
| (2.45) | |||
| (2.46) | |||
| (2.47) |
となることより、ベルヌーイ分布
| (2.48) | |||
| (2.49) | |||
| (2.50) | |||
| (2.51) | |||
| (2.52) | |||
| (2.53) | |||
| (2.54) |
となる.
Next: 選好と選択 Up: 離散型確率分布 Previous: モーメント母関数 digistats.net
平成23年5月2日
