
Next: 戦略の支配 Up: 戦略形ゲーム Previous: ミニマックス原理
ナッシュ均衡
定義 (最適応答 best response)
プレイヤー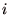 の戦略
の戦略 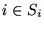 が他の
が他の 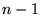 人のプレイヤーの戦略の組
人のプレイヤーの戦略の組
に対して、
であるとき最適応答(best response)であるという.
プレイヤー
| (6.8) |
| (6.9) |
定義 (ナッシュ均衡)
標準型ゲーム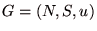 (
(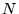 はプレーヤーの集合,
はプレーヤーの集合,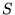 は戦略の集合,
は戦略の集合,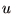 は利得の集合)において,戦略の組
は利得の集合)において,戦略の組 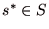 がナッシュ均衡であるとは,全てのプレイヤー
がナッシュ均衡であるとは,全てのプレイヤー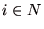 と全ての
と全ての
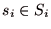 において,
において,
を満たすことを指す。但し,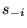 は
は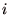 以外のプレイヤーの戦略の組を指す。
以外のプレイヤーの戦略の組を指す。
標準型ゲーム
| (6.10) |
すなわち、ナッシュ均衡とは,ゲーム理論の最も基本となる均衡概念で、ゲームに参加するすべてのプレーヤーが相互に他者の戦略を考慮に入れつつ、自己の利益を最大化するような戦略を実行したときに成立する均衡状態のことを意味する。
多数のプレーヤーが参加する非協力ゲームでは、あるプレーヤーがどのように戦略を変えても、自分以外のプレーヤーが戦略を変えない限り、それ以上には結果がよくならない混合戦略の組み合わせ(均衡点)が少なくとも1つ存在する。この均衡点では各プレーヤーが相互に最適戦略を取り合っている状況となり、すべてのプレーヤーが自分だけ戦略を変えても得にならないため、戦略の変更がない安定状態となる。
また、ナッシュ均衡はすべてのゲームに1つ以上あるが、1つしかないとは限らない。
更に、ナッシュ均衡はその状況における最適ではあっても、各プレーヤーにとって必ずしも最善な戦略、すなわち最大利得を保証するものではない。その典型例が「囚人のジレンマ」である。
ナッシュ均衡は、19世紀に活躍したフランスの数学者・経済学者のアントワーヌ・A・クールノー(Antoine Augustin Cournot)が論じた、複占市場における均衡状態(クールノー均衡)をn人に拡張したものといえる(クルーノー均衡は、クールノ=ナッシュ均衡とも呼ばれる)。また、ゲーム理論的にはゼロサム2人ゲームの均衡定理であるミニマックス定理の一般化となっている。
定理 (ゼロ和2人ゲームの鞍点 saddle point)
ゼロ和2人ゲームにおいて戦略の組である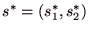 がナッシュ均衡であるための必要十分条件は、全ての
がナッシュ均衡であるための必要十分条件は、全ての
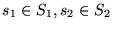 に対して、
に対して、
が成立することである.
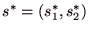 をゼロ和2人ゲームの鞍点(saddle point)という.
をゼロ和2人ゲームの鞍点(saddle point)という.
ゼロ和2人ゲームにおいて戦略の組である
| (6.11) |
まず、
| (6.12) |
| (6.13) |
| (6.14) |
| (6.15) |
| (6.16) |
| (6.17) |
| (6.18) |
Next: 戦略の支配 Up: 戦略形ゲーム Previous: ミニマックス原理 digistats.net
平成23年5月2日
