
Next: 次数付き辞書的順序 Up: 選好関係 Previous: 局所非飽和な選好の性質
効用関数
定義 (効用 utility)
一般に、貨幣額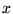 円に対して意思決定主体であるプレイヤーが持つ主観的評価を数値化した尺度
円に対して意思決定主体であるプレイヤーが持つ主観的評価を数値化した尺度 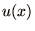 を貨幣に対する効用(utility)とよぶ.
を貨幣に対する効用(utility)とよぶ.
一般に、貨幣額
定義 (序数的効用と基数的効用)
- 序数的効用
- :順序のみに意味がある効用
- 基数的効用
- :数値事態に意味がある効用
- 序数的特性
- :任意の正の単調変換を加えても変化しない性質
単調増加性や強い擬凹性など. - 基数的特性
- :ある正の単調変換を加えると維持出来ない性質
2回微分可能な単調増加な強い擬凹性
定義 (期待効用 expected utility)
効用(utility)の期待値を期待効用とよぶ.
効用(utility)の期待値を期待効用とよぶ.
定義 (効用関数 utility function)
選好関係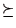 に対して、ある関数
に対して、ある関数
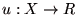 が、任意の行動計画
が、任意の行動計画 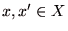 について、
について、
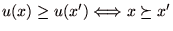
を満たすならば、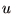 はこの選好関係を表現する効用関数である.
はこの選好関係を表現する効用関数である.
選好関係
を満たすならば、
定義 (序数的効用関数)
効用関数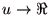 が選好関係
が選好関係 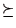 を表現するということは以下を意味する.
を表現するということは以下を意味する.
![$\forall x,x' \in X[x \succeq x' \Leftrightarrow u(x) \geq u(x')]$](./image/img171.png)
効用関数
定理 (表現定理)
混合集合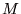 と
と 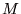 上の選好順序
上の選好順序 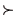 に対して選好順序の公理が成立するための必要十分条件は以下の通りである.
に対して選好順序の公理が成立するための必要十分条件は以下の通りである.
混合集合
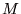 上の実数値関数
上の実数値関数 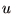 が存在して、
が存在して、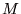 の任意の元
の任意の元 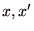 に関して、
に関して、
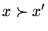 ならば
ならば
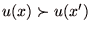 であり、逆も成り立つこと.
であり、逆も成り立つこと.
- 任意の
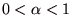 に対して、
に対して、
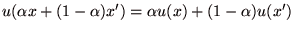
が成り立つこと.
定義 (フォン・ノイマン=モルゲンシュテルン効用関数 N-M utility function)
表現定理における2式を満たす実数値関数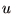 をフォン・ノイマン=モルゲンシュテルン効用関数という.
をフォン・ノイマン=モルゲンシュテルン効用関数という.
表現定理における2式を満たす実数値関数
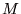 上の実数値関数
上の実数値関数 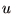 が存在して、
が存在して、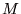 の任意の元
の任意の元 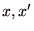 に関して、
に関して、
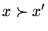 ならば
ならば
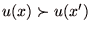 であり、逆も成り立つこと.
であり、逆も成り立つこと.
- 任意の
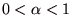 に対して、
に対して、
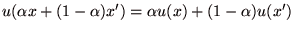
が成り立つこと.
定理 (一意性)
混合集合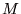 上の2つの実数値関数
上の2つの実数値関数 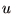 と
と 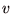 が表現定理の2式を満たすとする.
が表現定理の2式を満たすとする.
このとき、実数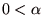 が存在して、集合
が存在して、集合 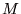 の任意の元
の任意の元 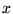 に対して、
に対して、
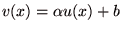
が成り立つ.
すなわち、フォン・ノイマン=モルゲンシュテルン効用関数は正の1次変換を除いて一意に定まる.
混合集合
このとき、実数
が成り立つ.
すなわち、フォン・ノイマン=モルゲンシュテルン効用関数は正の1次変換を除いて一意に定まる.
定義 (籤 lottery)
リスクを含む選択対象を籤(くじ)と呼ぶ.この籤(くじ)の結果を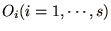 とし、
とし、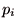 を結果
を結果 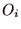 が実現する確率とすると、籤(くじ)は以下のように表すことが出来る.
が実現する確率とすると、籤(くじ)は以下のように表すことが出来る.
![$z = [O_{1},...O_{s};p_{1},...,p_{s}]$](./image/img181.png)
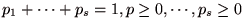
リスクを含む選択対象を籤(くじ)と呼ぶ.この籤(くじ)の結果を
定義 (期待効用仮説 expected utility hypothesis)
プレイヤー(=意思決定主体)は複数の選択肢に関して、
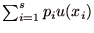
を最大化するように選択肢を選択する.
プレイヤー(=意思決定主体)は複数の選択肢に関して、
を最大化するように選択肢を選択する.
digistats.net
平成23年5月2日
