フィッシャ〖の给及
赖蹋附哼擦猛(Net Present Value) †
介袋抨获を I とすると、赖蹋附哼擦猛∈NPV∷は肌のようになる。
=====
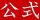 \[NPV=-I+\frac{{C}_{1}}{(1+r)}+\frac{{C}_{2}}{{(1+r)}^{2}}+ˇˇ\frac{{C}_{n}}{{(1+r)}^{n}}\]
\[NPV=-I+\frac{{C}_{1}}{(1+r)}+\frac{{C}_{2}}{{(1+r)}^{2}}+ˇˇ\frac{{C}_{n}}{{(1+r)}^{n}}\]
=====
- 赖蹋附哼擦猛がプラスならば抨获を乖う。
- 剩眶のキャッシュフロ〖の附哼擦猛は、それぞれのキャッシュフロ〖の附哼擦猛の圭纷となる。
柒婶箭弊唯 †
肌の及を塔たす r を柒婶箭弊唯という。
=====
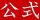 \[I=\frac{{C}_{1}}{(1+r)}+\frac{{C}_{2}}{{(1+r)}^{2}}+ˇˇ\frac{{C}_{n}}{{(1+r)}^{n}}\]
\[I=\frac{{C}_{1}}{(1+r)}+\frac{{C}_{2}}{{(1+r)}^{2}}+ˇˇ\frac{{C}_{n}}{{(1+r)}^{n}}\]
=====
附哼擦猛(Present Value) †
コンソル耗の附哼擦猛(笔底年驰钳垛) †
=====
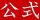 \[PV=\frac{{C}_{1}}{(1+r)}+\frac{{C}_{2}}{{(1+r)}^{2}}+ˇˇ\frac{{C}_{n}}{{(1+r)}^{n}}=\frac{C}{r}\]
\[PV=\frac{{C}_{1}}{(1+r)}+\frac{{C}_{2}}{{(1+r)}^{2}}+ˇˇ\frac{{C}_{n}}{{(1+r)}^{n}}=\frac{C}{r}\]
=====
キャッシュフロ〖が喇墓する眷圭(笔底喇墓钳垛) †
=====
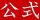 \[PV=\frac{{C(1+g)}}{(1+r)}+\frac{{C(1+g)^2}}{{(1+r)}^{2}}+ˇˇ\frac{{C(1+g)^n}}{{(1+r)}^{n}}=\frac{C}{r-g}\]
\[PV=\frac{{C(1+g)}}{(1+r)}+\frac{{C(1+g)^2}}{{(1+r)}^{2}}+ˇˇ\frac{{C(1+g)^n}}{{(1+r)}^{n}}=\frac{C}{r-g}\]
=====
キャッシュフロ〖が办年袋粗费鲁する眷圭(铜袋年驰钳垛) †
=====
 \[PV=C(\frac{1}{r}-\frac{1}{r(1+r)^n})=\frac{C}{r}(1-\frac{1}{(1+r)^n})\]
\[PV=C(\frac{1}{r}-\frac{1}{r(1+r)^n})=\frac{C}{r}(1-\frac{1}{(1+r)^n})\]
=====

