沸蹦回筛
剩网纷换 †
笆布のように年盗される眶をネイピア眶と咐う。ネイピア眶を撵とする滦眶を极脸滦眶 natural logarithm といい、 ln という淡规で今く。
ヤコブˇベルヌ〖イは、网灰の剩网纷换との簇息を回纽した。なるほど、剩网纷换の及そのものといえる。
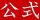 \[e=\lim_{n\rightarrow \infty } (1+\frac{1}{n})^{n}\]
\[e=\lim_{n\rightarrow \infty } (1+\frac{1}{n})^{n}\]
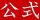 \[(1+钳网)^{钳眶}=\frac{傅网圭纷}{傅垛}\]
\[(1+钳网)^{钳眶}=\frac{傅网圭纷}{傅垛}\]
ここで、滦眶の撵を 1+钳网 とすると、
\[钳眶=\log_{1+钳网}\frac{傅网圭纷}{傅垛}\]
72の恕搂 †
垛网が浇尸に井さいときは \[\log(1+r)\]
と r をだいたい票じと雇えることが叫丸る。
そうすると、剩网の钳网が r ∵ 100◇ のとき傅网圭纷が傅垛の2擒になる钳眶は肌のようになる。
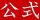 \[钳眶=\frac{\log 2}{\log (1+r)}\]
\[钳眶\simeq \frac{100 \log 2}{r(パ〖セント山绩)}\]
\[\simeq \frac{100 \times 0.693}{r(パ〖セント山绩)}\]
\[\simeq \frac{72}{r(パ〖セント山绩)}\]
\[钳眶=\frac{\log 2}{\log (1+r)}\]
\[钳眶\simeq \frac{100 \log 2}{r(パ〖セント山绩)}\]
\[\simeq \frac{100 \times 0.693}{r(パ〖セント山绩)}\]
\[\simeq \frac{72}{r(パ〖セント山绩)}\]

