算術平均
「データが一体どんな特質を持つものなのかを表す物差しとしては、
があるね」
「中心の尺度というのは、データという集合の中心がどこにあるのかってことよね。
良く知られたものには、
があるわ」
「普通に使われるのは平均。特に算術平均だね。まぁ、平均と言ったら算術平均。
ここに、2004年3月31日の大手情報通信会社の東京証券取引所での株価がある。
| NEC(D1) |
863 |
| 富士通(D2) |
657 |
| 沖電気(D3) |
498 |
| ソニー(D4) |
4,380 |
| 松下(D5) |
1,612 |
| 日立(D6) |
803 |
| 東芝(D7) |
474 |
| 三菱電機 |
588 |
この株価の平均は1,234。
エクセルだと、AVERAGE(D1:D7)って関数を使うと計算出来る。
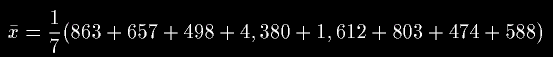
を計算しているんだけどね。これを一般的に書くと、
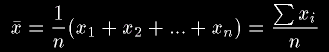
となるね」
「ちょっと待って。
そのｘっていうのはデータのことよね。それは良いとして、なんでｘの上に変てこなモノがくっ付いているの？」
「バレタぁ？
今の例は情報通信企業の株価のデータ。しかも、2004年3月31日という特定の日のデータ。その背後には、実際には観察されないデータの集合(母集団)があると考えることが出来る。というか、そういうものを考えることにするんだけど、そうした母集団に対して観測されたデータ(標本)の平均なんだよっていうことを意味しているんだ」
